√70以上 辺の比 面積比 156573-辺の比 面積比
平行線と比の利用、辺の長さを求める問題をパターン別解説!←今回の記事 木の高さを求める方法について解説! 中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比!
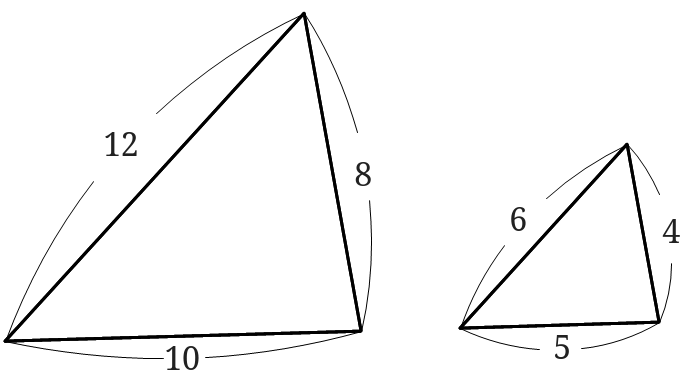
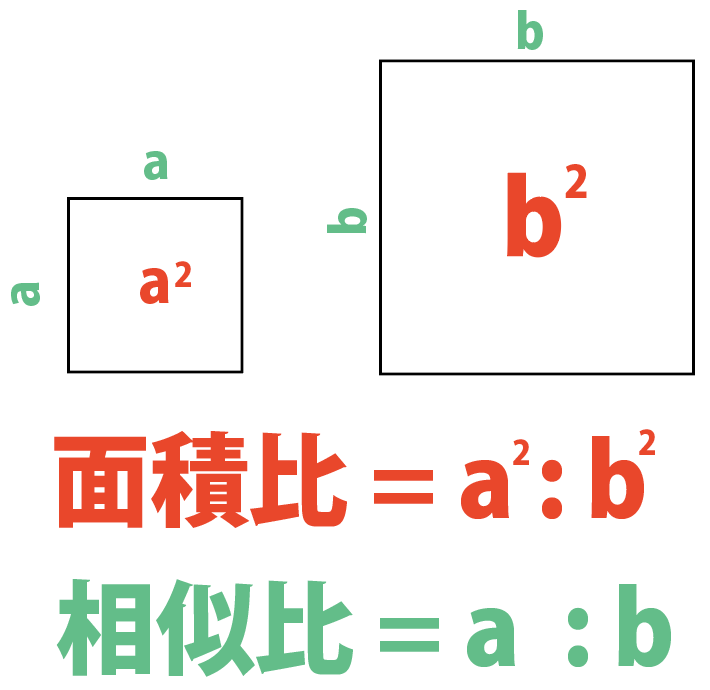
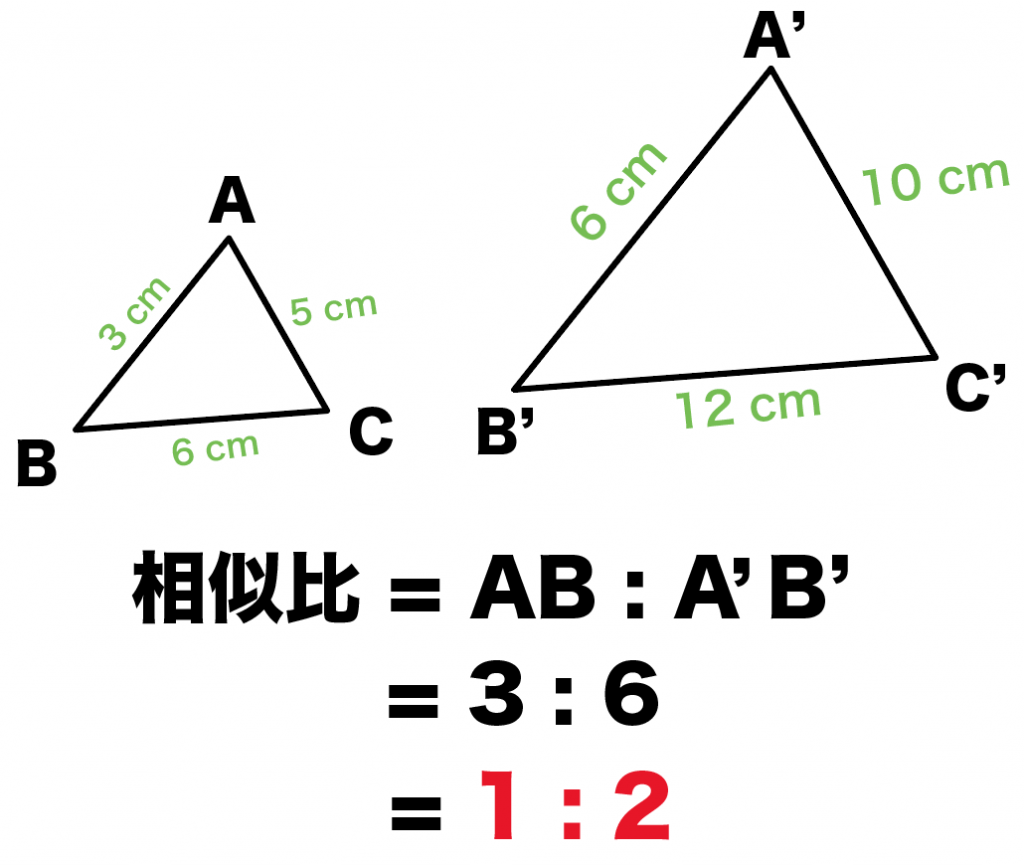
辺の比 面積比- いろいろな三角形の面積を比較しながら、最終的な面積の比較にもっていきます。 三角形pqr の辺の延長線上で、比がわかっている bq : qr : rf = 2 : 2 : 1 に注目します。 次に、cr : rp : pd = 2 : 2 : 1 に注目して、体積の比 1 相似な平面図形の面積 (1 時間) 〈目標〉 相似な平 面図形 比と積 関係を理解する。 問題 左の図のア,イについて, 面積が大きいのはどっち? 相似な平面図形の相似 比,面積比について,具 体的な事象から一般的に いえることを
辺の比 面積比のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  |  |
「辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 | ||
「辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  |  |
「辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  |  |
「辺の比 面積比」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
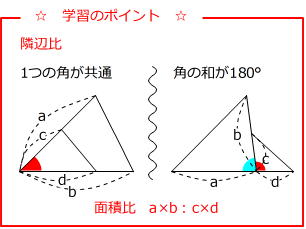
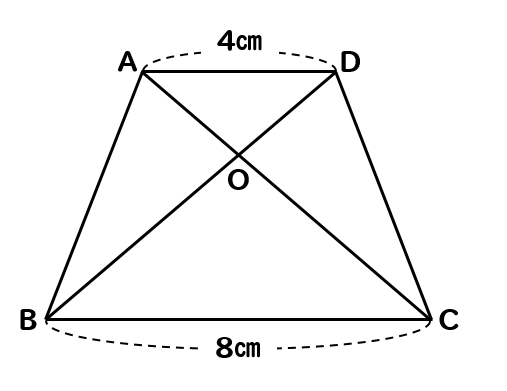
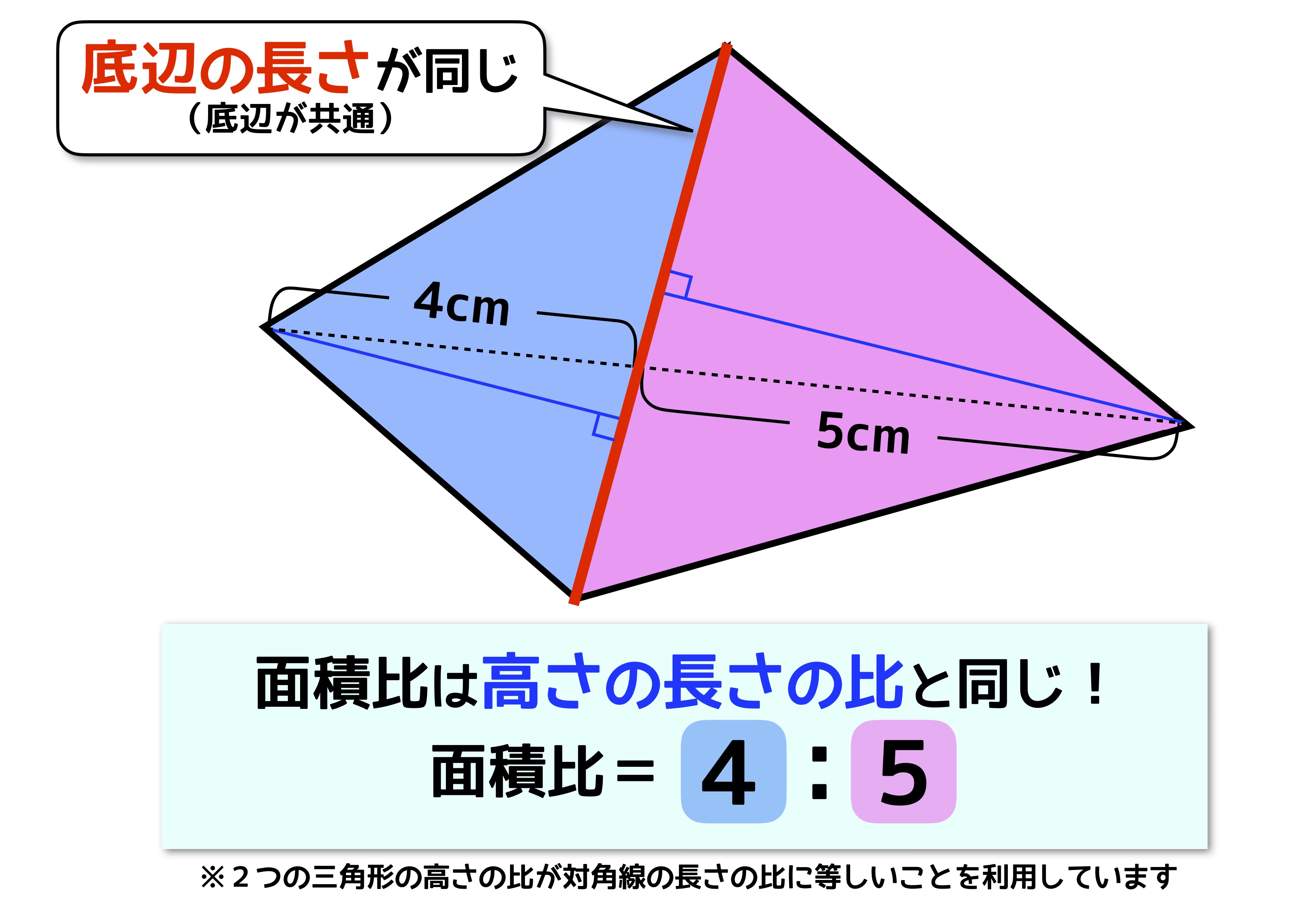
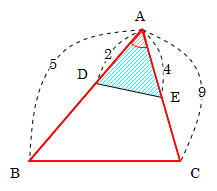
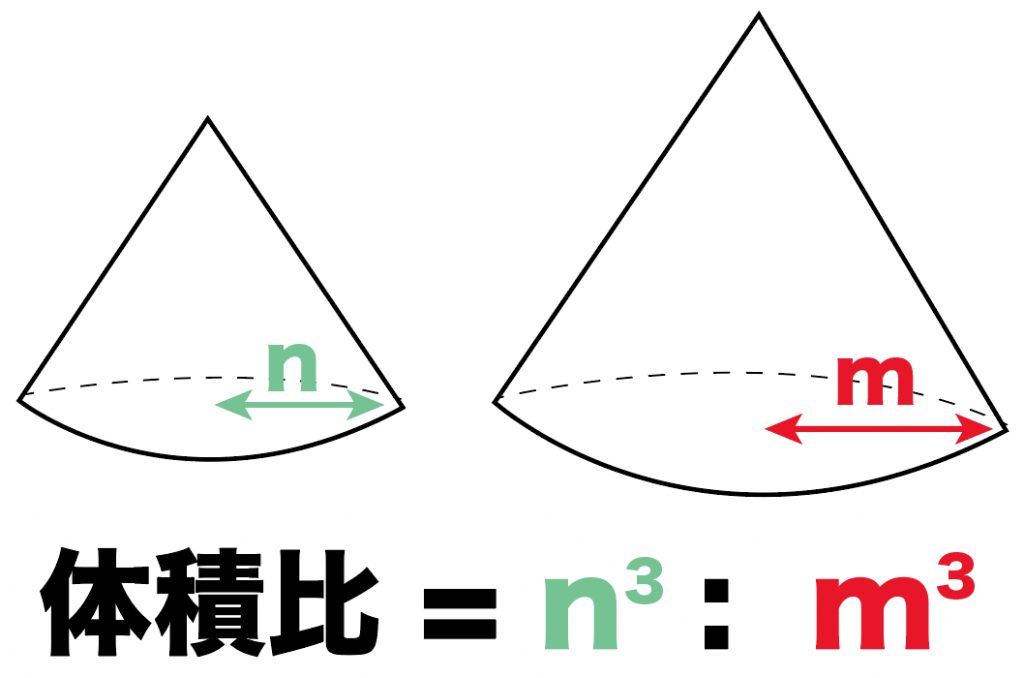
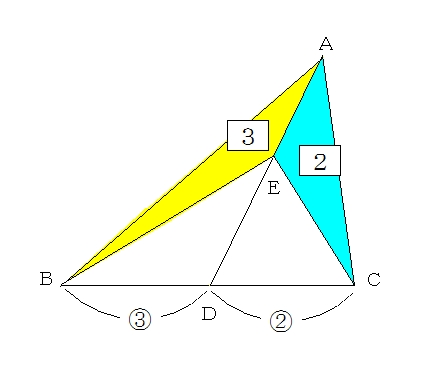
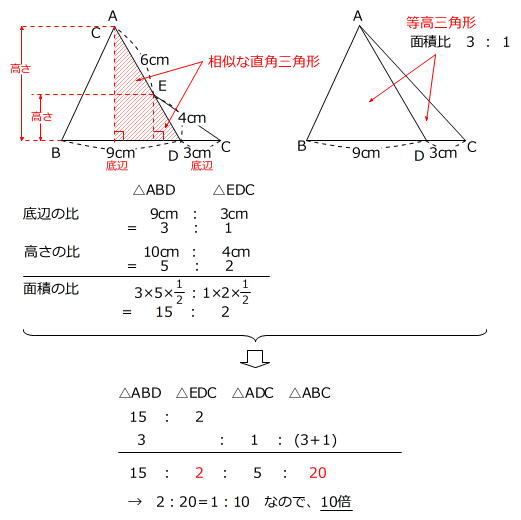
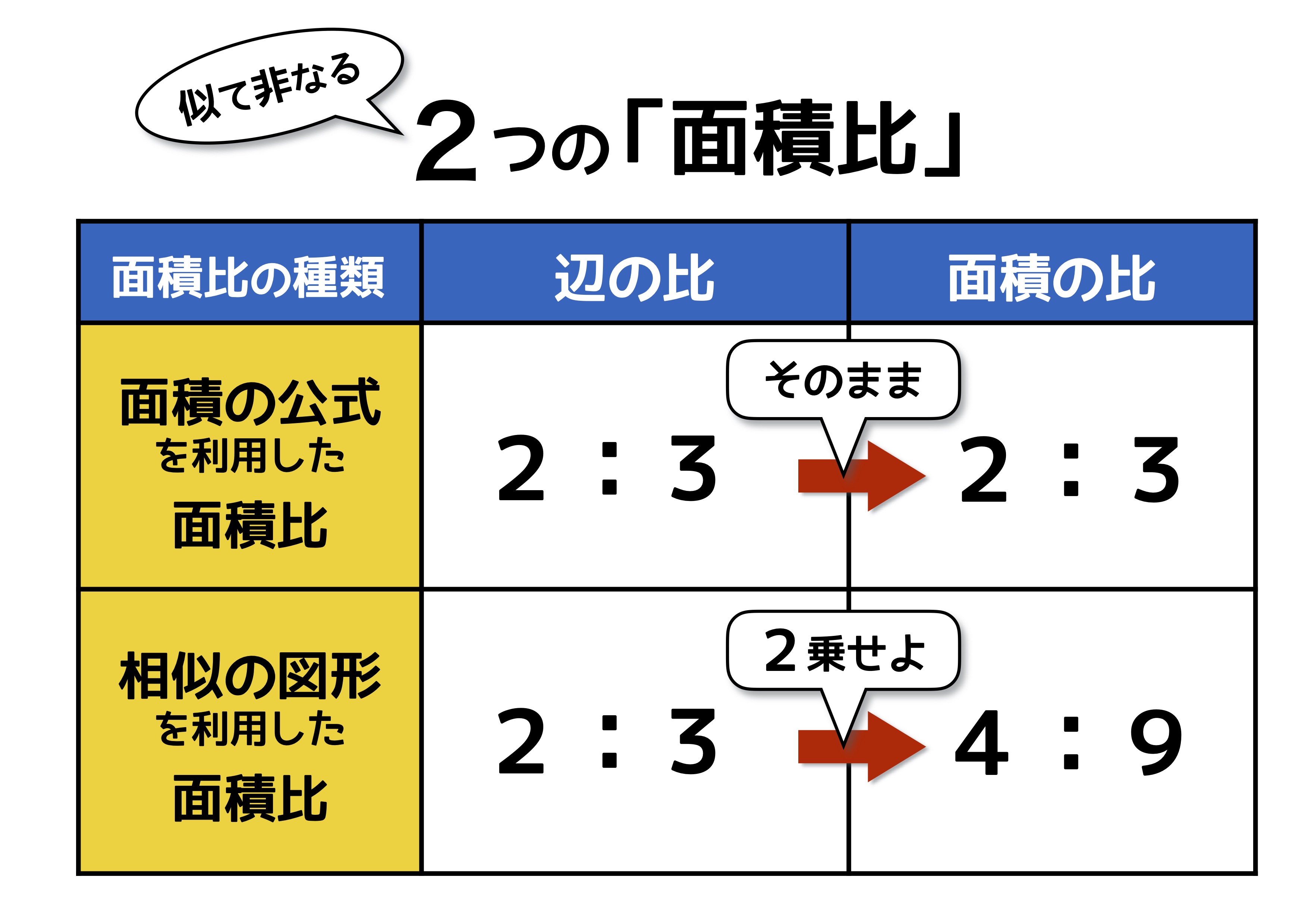
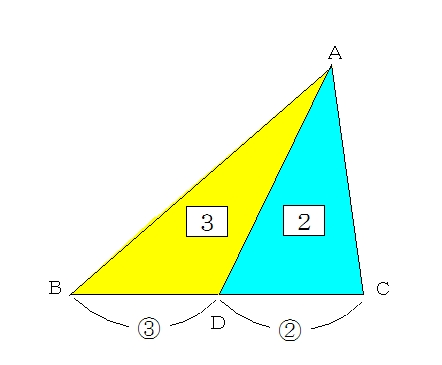
空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m 2 n 2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底 あとは面積比を考えればおしまいですね。辺の比が分かっているので、面積比も求めることができます。 三角形 ABC の面積を S とすると、 $\mathrm{ BD }\mathrm{ DC }=54$ なので、三角形 ABD の面積は $\dfrac{5}{9}S$ 、三角形 ACD の面積は $\dfrac{4}{9}S$ となります。
Incoming Term: 辺の比 面積比, 辺の比 面積比 関係,
コメント
コメントを投稿